Application of a deep-learning neural network for image reconstruction from a single-pixel infrared camera

• Institute of Electronics, Lodz University of Technology, Al. Politechniki 6, 90-924 Lodz, Poland

Abstract

The article presents the simulation results of a single-pixel infrared camera image reconstruction obtained by using a convolutional neural network (CNN). Simulations were carried out for infrared images with a resolution of 80 × 80 pixels, generated by a low-cost, low-resolution thermal imaging camera. The study compares the reconstruction results using the CNN and the ℓ₁ reconstruction algorithm. The results obtained using the neural network confirm a better quality of the reconstructed images with the same compression rate expressed by the peak signal-to-noise ratio (PSNR) and structural similarity index measure (SSIM).

Introduction

Nowadays, infrared thermography (IRT) is becoming more and more popular thanks to its wide range of applications, among which are: mechanical engineering [1], energy saving [2], biology [3], cultural heritage [4], envi-ronment [5], medicine [6], electronics [7], heat transfer [8], chemistry [9] physiology [10], materials evaluation [11], and 3D vision [12]. IR technique allows the registration of thermal radiation emitted by various objects. IRT uses mainly two ranges of electromagnetic radiation spectrum: long-wave infrared (LWIR) 7–14 μm and medium-wave infrared (MWIR) 3–5 μm. There are two main types of IR sensors used in thermal imaging cameras: uncooled microbolometers and cooled photon detectors. Both are manufactured as detector matrices called focal plane arrays (FPA). A typical microbolometer IR detector can be made of different materials, such as a-Si or VOx. In turn, cooled detectors often operating at a temperature of about 77 K are made of narrow-bandgap semiconductors, such as HgCdTe or InSb [13]. The FPAs suffer from the problem of non-uniformity (NU). NU is caused by the dispersion of detector parameters and the presence of dead pixels in an array. The most commonly used method of reducing NU in the IR cameras is a two-point correction [14, 15].

The single-pixel camera (SPC) is a solution to replace the array with a single detector [16, 17]. The lack of non-uniformity correction (NUC) is an important advantage of the SPC. It is worth emphasizing that very expensive hyperspectral IR systems can be replaced with single or multi-sensor devices operating on the SPC principle. The SPC concept is based on compressive sensing [18], which reconstructs the original data from a small number of samples below the Nyquist frequency limit [19]. This is generally possible due to the redundancy inherent in most signals and images. The first SPC implementation was made for optical image processing [20]. Today, this technique is spreading across a variety of applications, including IR and near IR imaging, acoustics, holography, and signal processing [21]. The problem of signal reconstru-ction from a small number of samples concerns non-linear optimization. In many practical cases, it is worth using a transform coding approach, e.g., with wavelet or discrete cosine transform to obtain a sparse representation of a signal in another domain. As a result, it is possible to reduce the problem mathematically to the sparse solution of an underde-termined linear system [22]. It leads directly to linear prog-ramming, which is based on minimizing the ℓ₁ norm [23].

This is the well-known ℓ₁-magic algorithm available online [24]. A solution based on deep learning is our proposal to reconstruct a sparse IR image [25]. Artificial intelligence algorithms are increasingly used for advanced thermal imaging, e.g., to improve the NUC of IR images, especially in bolometer uncooled cameras [26, 27], or to increase its resolution using so-called super-resolution techniques [28, 29]. The application of SPC in the terahertz wave-length domain is a very promising low-cost solution [30].

Most of the modern applications use different deep-learning networks. Among many frequently used models, there are ResNet, AlexNet, VGGNet, GoogleNet, MobileNet, which are predefined and already pretrained, typically by visual or other-modality images. The manufacturers can adapt them to a specific problem by final up-learning using the IR images. A novel application of a convolutional neural network (CNN) for medical screening has been recently published using IRT for monitoring the thermal provocation test [31].

Although the learning process is sometimes very time-consuming on powerful servers using advanced graphics processing unit (GPU) modules, the classification or regression processes can be performed in real time. In the case of SPC, the reconstruction process involves the use of an appropriate algorithm that will guarantee the best reconstruction results. The authors’ goal is to use a spatial light modulator (SLM) and then reconstruct the image using a simple CNN [32]. Before building a real system, simulations should be performed to select the optimal solution for implementation. The main results presented in this article are a quantitative comparison of the performance of the CNN and ℓ₁ – magic algorithms. The advantages and disadvantages of both solutions are highlighted in this work.

Methods

Single-pixel camera (SPC) concept

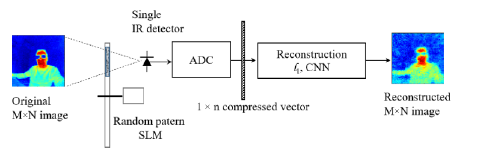
The SPC operates based on a simple principle. IR radiation emitted by an object passes through the SLM and then is focused on a single detector. In a typical application, no lens is needed. In visual systems, the SLM can be implemented using shutters with randomly distributed openings or electrically-controlled micromirrors [15], or LCD arrays [16]. As a result, for each set of openings, the average radiation intensity is acquired. The measurements are saved as a compressed vector with a much lower number of samples compared to the number of pixels in the corresponding IR image.

The original images are then reconstructed using a compressive sensing algorithm as presented in Fig. 1.

‌

CNN-based compressive sensing reconstruction

Compressive sensing is a useful technique that allows to simplify the hardware of a data acquisition system. On the other hand, this technique requires the application of an advanced signal processing. In the visual image processing, the ℓ₁ magic algorithm is widely used [33]. A new approach presented in this research is based on deep-learning neural network image reconstruction. A simple CNN based on the decoder architecture was used as shown in Fig. 2.

‌

The proposed CNN architecture is a result of a certain number of trials and, at this stage of research, it meets the compromise between quality of reconstructed images, calculus complexity, and computational requirements for implementation. The important advantage of SPC is low-power and low-cost electronics for signal processing. One of the possible solutions is the application of a hardware-support processing system, e.g., using a field-programmable gate array (FPGA) technology. The proposed model of CNN uses a concept of the residual network with long skip connections [34]. It can prevent the learning process of such a network from vanishing/ exploding gradients and, finally, from slowing and blocking learning [35]. The details of the CNN applied are presented in Table 1.

‌

Training and validation

The size and quality of training and validation datasets are key issues for the proper development of a deep-learning neural network. Three different CNN learning datasets were tested during the study. The first test used the dataset of 1000 IR images (IRdataset) of 80 × 80 resolution [34]. The IRdataset was divided for training/validation subsets of 800/200. Transfer training was then tested using 7200 visual images (VISdataset) cropped to 80 × 80 resolution.

This set was divided into 6000/1200 images for training and validation. Next, 80 × 80 synthetic images were generated in the form of geometrical sharp figures: rectangles, triangles, polygons, ellipses, arcs, polyline curves, and different figure slices with different sizes, colours, orientations (SYNTHdataset). The intention of using sharp figures for training was to reduce the blurring of edges of the reconstructed IR images. In this case, two datasets with 5000 and 1000 images were selected for training and validation.

After several learning tests were performed, the final mixed dataset (MIX dataset) of images was chosen. It contained 10 000 images for training equally divided (5000/5000) into visual and synthetic parts. For validation, 2000 images were selected in the equal proportion (1000/1000) of visual and synthetic images. In addition, 50 IR images that were not used for training or validation were selected for final testing. The SPC simulation was implemented as follows. Each 80 × 80 image was transformed using shutters with randomly distributed openings in an 80 × 80 raster. The summed radiation signal for each shutter was then calculated. The simulation was carried out for different number of shutters with openings (different compression ratio): 500, 1000, 1500. It allowed to verify the algorithm performance for various compression ratios of 7.8, 15.6, and 23.4%. For training, each image was compressed to a 500-, 1000-, or 1500-element vector. Generated vectors were added to the CNN training and testing datasets. The learning was carried out using the descent gradient optimizer from the Keras library and implemented in the TensorFlow – artificial intelligence environment [36]. In addition, the augmentation was applied during the training of CNN using 9 randomly selected image transforms:

• albumentations.InvertImg (p  =  0.2),
• albumentations.HorizontalFlip (p = 0.2),
• albumentations.RandomBrightnessContrast (p = 0.2),
• albumentations.Superpixels (p = 0.2),
• albumentations.Posterize (p = 0.2),
• albumentations.GaussNoise (p = 0.2),
• albumentations.Sharpen (p = 0.2), alpha = (0.2, 0.4), lightness = (0.5, 0.6),
• albumentations.MotionBlur (p = 0.2),
• albumentations.ShiftScaleRotate (p = 0.2).

Results

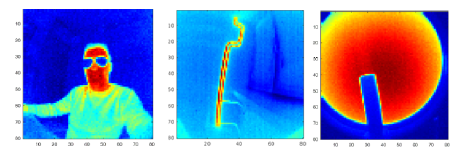
Simulations were performed for 3 different compression ratios CR = 7.8125%, 15.6250%, and 23.4375%. This means that the original 80 × 80 IR images have been compressed into vectors of 500, 1000, and 1500 elements. Each element was calculated as the average value of randomly selected pixels from the 80 × 80 IR image. A test dataset of 50 IR images acquired by a self-developed low-cost camera [37] was used to average the results and validate quantitatively the image decompression. To present the difference in the operation of ℓ₁ and CNN reconstruction algorithms, 3 IR images were selected for detailed analysis – Fig. 3.

‌

In order to compare the results of the image reconstru-ction, the widely used parameters of peak signal-to-noise ratio (PSNR) in decibels and structural similarity index measure (SSIM) [38] were used. The SSIM parameter [39] seems to be more objective for image comparison. It considers 3 independent image features: luminance, contrast, and image structure [23]. The luminance is the average pixel value in each image, thus the luminance comparison can be represented by (1):

\( l(x, y)=\frac{2 \mu_x \mu_y+C_1}{\mu_x^2+\mu_y^2+C_1} \) (1)

where C1 is the small constant for numerical stability, μ_x . and μ_y are the pixel sample means of 𝑥 and 𝑦 respectively. Similarly, the constants C2 and C3 are introduced in the following equations for contrast and structure measures. The values of all constant parameters are selected exper-imentally. Contrast is calculated based on the standard deviation (σ), shown in (2):

\( \mathrm{c}(x, y)=\frac{\left(2 \sigma_x \sigma_y+C_2\right)}{\left(\sigma_x^2+\sigma_y^2+C_2\right)} \) (2)

The structure index uses the covariance σxy normalized image variance, as shown in (3):

\( \mathrm{s}(x, y)=\frac{\sigma_{x y}+C_3}{\sigma_x \sigma_y+C_3} \) (3)

Finally, the three components are connected by (4):

\( \operatorname{SSIM}(x, y)=[l(x, y)]^\alpha *[c(x, y)]^\beta *[s(x, y)]^y \) (4)

where α, β, and γ parameters are experimentally selected.

Examples of ℓ₁ reconstruction

This research is the first step for development of a real IR SPC for dedicated applications, e.g., gas leak detection. Cooled and uncooled IR systems have become more and more popular mainly in industrial environments [38]. Such systems equipped with matrix sensors have been already applied for optical gas imaging (OGI) [40]. In order to achieve this goal, the comparative simulations using well-known ℓ₁ and the proposed CNN-based decompression algorithms were carried out for different compression rates (CR). The example results obtained by using the ℓ₁ reconstruction algorithm for different CR are presented in Fig. 4.

‌

CNN-based reconstruction results

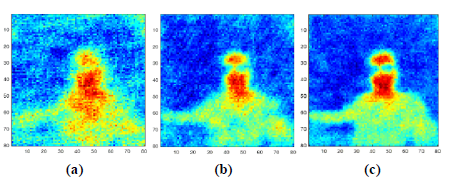
As noted above, the quantitative results are shown for a 50-item set of IR test images that are not used for training or validation. The first examples (Fig. 5) show a person wearing glasses, which is qualitatively better decompressed compared to the results of the ℓ₁ reconstruction. The reconstructed images are sharper and contain more detail. It can be seen that the relatively higher performance of the CNN-based algorithm relates to the higher compression ratio. The result of the ℓ₁ algorithm for CR = 7.8125% is rather poor, noisy, and blurry, as shown in Fig. 4(a).

‌

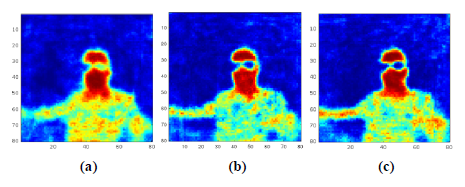
The next example shows the worst-case decompression performed by the proposed CNN. It is a thin, warm, curved tube shown in Fig. 6. Qualitatively, the results are satisfactory, but this is not confirmed by the value of the PSNR measure. This is due to the large, relatively homogeneous background, which is reconstructed with a significant offset as presented in Fig. 6.

‌

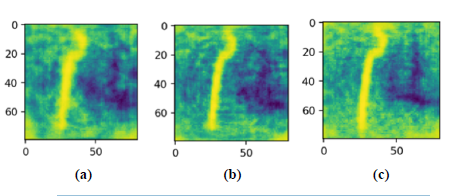
The last example shows a round black body that fills the main part of the observed scene – Fig. 7. Surprisingly, for all compression ratios, the similarity indexes are very close to each other. This is because the main part of the IR scene is covered with the higher temperature object. As a result, the spread of temperature values is relatively large, and the normalization applied by CNN during pre-processing does not significantly alter the original input image.

‌

Finally, for a quantitative assessment of the proposed approach for a compressive sensing image reconstruction performed in the form of CNN, the average values of the similarity indexes for 50 IR test images are calculated. The results are presented in Table 2.

‌

Discussion

Analysing the results presented in the previous chapter, it can be concluded that deep learning is a promising option for image reconstruction in a single-pixel thermal imaging based on compression sensing. In most simulations, the results are competitive with those obtained using the ℓ₁ algorithm. The greater advantage of using the deep-learning approach is noticeable with a higher compression ratio as shown in Fig. 8.

‌

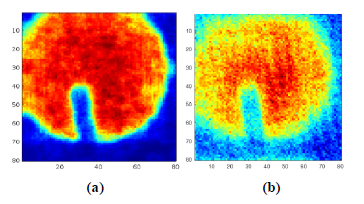
In general, the deep-learning image reconstruction is not invariant concerning mean value and contrast due to the normalization used while the input dataset for learning is created. This means that the proposed solution is rather recommended for observation cameras that are used to detect and identify objects. In most cases, the reconstructed image is over-contrasted, which results in an underesti-mation of the PSNR value. To enlarge the PSNR factor, the contrast has to be reduced and the mean value of the image needs to be properly adjusted. It enlarges PSNR value significantly. The result of such an operation is presented in Fig. 9.

‌

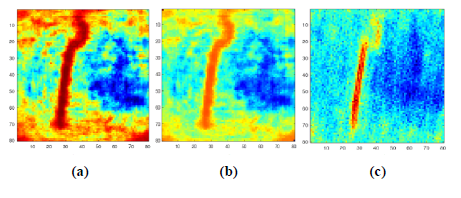
Conclusions

The single-pixel IR camera is an optical system consisting of an SLM and a single IR photodetector that measures the average radiation intensity of the scene corresponding to the SLM pattern. It enables the construction of low-cost, energy-saving, small and high-quality imaging devices applicable in a wide range of applications, such as remote and hyperspectral imaging, as well as object and gas detection. A simple CNN for image reconstruction for SPC was simulated. The presented results show superior operation of a deep-learning approach compared to the well-known and widely used ℓ₁-magic reconstruction, especially for high-compression ratios. On the other hand, the image transformation made by CNN is not invariant concerning the mean value of the image and its contrast. It is due to the normalization used by CNN for faster and better learning. Basically, in practice, a CNN-based SPC provides sharper reconstructed images with clearly visible fine details and higher contrast. Consequently, the proposed solution is more suitable for IR surveillance systems for a better more reliable detection and identification of objects. Thermal imaging cameras are relatively expensive today, which limits their usefulness. The development of a single-detector thermal imaging camera would make thermal imaging more popular and useful. The exchange of the single-pixel sensor easily allows to adjust the wavelength characteristics for different gases.

Acknowledgements

The authors declare no conflicts of interest.

References

1. ‌Trofimov, A. A., Watkins, T. R., Muth, T. R., Cola, G. M. & Wang,H. Infrared thermometry in high temperature materials processing: influence of liquid water and steam. Quant. Infrared Thermogr. J. 20, 123–141 (2023) https://doi.org/10.1080/17686733.2022.2043617

2. ‌Kim, C., Park, G., Jang, H. & Kim, E.-J. Automated classification of thermal defects in the building envelope using thermal and visible images. Quant. Infrared Thermogr. J. 20, 106–122 (2023). https://doi.org/10.1080/17686733.2022.2033531

3. ‌Gabbi, A. M. et al. Use of infrared thermography to estimate enteric methane production in dairy heifers. Quant. Infrared Thermogr. J. 19, 187–195 (2022). https://doi.org/10.1080/17686733.2021.1882075

4. ‌Tao, N., Wang, C., Zhang, C. & Sun, J. Quantitative measurement of cast metal relics by pulsed thermal imaging. Quant. Infrared Thermogr. J. 19, 27–40 (2022). https://doi.org/10.1080/17686733.2020.1799304

5. ‌Shoa, P., Hemmat, A., Amirfattahi, R. & Gheysari, M. Automatic extraction of canopy and artificial reference temperatures for determination of crop water stress indices by using thermal imaging technique and a fuzzy-based image-processing algorithm. Quant. Infrared Thermogr. J. 19, 85–96 (2022). https://doi.org/10.1080/17686733.2020.1819707

6. ‌Ervural, S. & Ceylan, M. Thermogram classification using deep siamese network for neonatal disease detection with limited data. Quant. Infrared Thermogr. J. 19, 312–330 (2022). https://doi.org/10.1080/17686733.2021.2010379

7. ‌Yoon, S. T., Park, J. C. & Cho, Y. J. An experimental study on the evaluation of temperature uniformity on the surface of a blackbody using infrared cameras. Quant. Infrared Thermogr. J. 19, 172–186 (2022). https://doi.org/10.1080/17686733.2021.1877918

8. ‌Yixian, D., Dexin, H., Zewen, D. & Shuliang, Y. Non-destructive evaluation method for thermal parameters of prismatic Li-ion cell using infrared thermography. Quant. Infrared Thermogr. J. 20, 14– 24 (2023). https://doi.org/10.1080/17686733.2021.2010380

9. ‌Goetten de Lima, G. et al. Effect of unidirectional freezing using a thermal camera on polyvinyl (alcohol) for aligned porous cryogels. Quant. Infrared Thermogr. J. 18, 177–186 (2021). https://doi.org/10.1080/17686733.2020.1732735

10. ‌Koroteeva, E. Yu. & Bashkatov, A. A. Thermal signatures of liquid droplets on a skin induced by emotional sweating. Quant. Infrared Thermogr. J. 19, 115–125 (2022). https://doi.org/10.1080/17686733.2020.1846113

11. ‌Kidangan, R. T., Krishnamurthy, C. V. & Balasubramaniam, K. Detection of dis-bond between honeycomb and composite facesheet of an inner fixed structure bond panel of a jet engine nacelle using infrared thermographic techniques. Quant. Infrared Thermogr. J. 19, 12–26 (2022). https://doi.org/10.1080/17686733.2020.1793284

12. ‌Schramm, S., Osterhold, P., Schmoll, R. & Kroll, A. Combining modern 3D reconstruction and thermal imaging: generation of large- scale 3D thermograms in real-time. Quant. Infrared Thermogr. J. 19, 295–311 (2022). https://doi.org/10.1080/17686733.2021.1991746

13. ‌Rogalski, A. Infrared Detectors, 2nd ed. (CRC Press, Boca Raton, 2011).

14. ‌Higham, C. F, Murray-Smith, R., Padgett, M. J. & Edgar, M. P. Deep learning for real-time single-pixel video. Sci. Rep. 8, 2369 (2018). https://doi.org/10.1038/s41598-018-20521-y

15. ‌Baraniuk, R. G. Compresive sensing. IEEE Signal Process. Mag. 24, 118–121 (2007). https://doi.org/10.1109/MSP.2007.4286571

16. ‌Yi, K. et al. Novel LCDs with IR-sensitive backlights. J. Soc. Inf.Disp.19, 48–56 (2011). https://doi.org/10.1889/JSID19.1.48

17. ‌Kim, B. H., Kim, M. Y. & Chae, Y. S. Background registration- based adaptive noise filtering of LWIR/MWIR imaging sensors for UAV applications. Sensors 18 60 (2018). https://doi.org/10.3390/s18010060

18. ‌Tralic, D. & Grgic, S. Signal Reconstruction Via Compressive Sensing. in 53rd International Symposium Elmar-2011 5–9 (IEEE, 2011).

19. ‌Candes, E., Romberg, J. & Tao, T. Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information. IEEE Trans. Inf. Theory 52, 489–509 (2006). https://doi.org/10.1109/TIT.2005.862083

20. ‌Bengio, Y., Simard, P. & Frasconi, P. Learning long-term dependencies with gradient descent is difficult. IEEE Trans. Neural Netw. 5, 157–166 (1994). https://doi.org/10.1109/72.279181

21. ‌Gerstoft, P., Mecklenbrauker, Ch. F., Seong, W. & Biancol, M. Introduction to compressive sensing in acoustic. J. Acoust. Soc. Am. 143, 3731–3736 (2018). https://doi.org/10.1121/1.5043089

22. ‌Gibson, G. M., Johnson, S. D. & Padgett, M. J. Single-pixel imaging 12 years on. Opt. Express 28, 28190–28208 (2020). https://doi.org/10.1364/OE.403195

23. ‌Kłosowski, G. et al. Using machine learning in electrical tomography for building energy efficiency through moisture detection. Energies 16, 1818 (2023). https://doi.org/10.3390/en16041818

24. ℓ₁-magic. (2023)‌https://candes.su.domains/software/l1magic/examples.html

25. ‌Minkina, W. & Dudzik, S. Infrared Thermography: Errors and Uncertainties, 1st Ed. (Wiley, 2009).

26. ‌Szajewska, A. Simulation of the operation of a single pixel camera with compressive sensing in the long-wave infrared. Pomiary Autom.Robot. 25, 53–60 (2021). https://doi.org/10.14313/PAR_240/53

27. ‌Strąkowski, R. & Więcek, B. Temperature Drift Compensation in Metrological Microbolometer Camera Using Multi Sensor Approach. in 13th Quantitative Infrared Thermography Conference (QIRT) 791–798 (QIRT Council, 2016). https://doi.org/10.21611/qirt.2016.126

28. ‌Shorten, C. & Khoshgoftaar, T. M. A survey on image data augmentation for deep learning. J. Big Data 6, 60 (2019). https://doi.org/10.1186/s40537-019-0197-0

29. ‌Więcek, P. & Sankowski, D. A New Deep-Learning Neural Network for Super-Resolution Up-Scaling of Thermal Images. in 15th Quantitative InfraRed Thermography Conference 1–7 (QIRT Council, 2020). http://www.qirt.org/archives/qirt2020/papers/134.pdf

30. ‌Valles, A., He, J., Ohno, S., Omatsu, T. & Miyamoto, K. Broadband high-resolution terahertz single-pixel imaging. Opt. Express 28, 28868–28881 (2020). https://doi.org/10.1364/OE.404143

31. ‌Strąkowska, M. & Strzelecki, M. Thermal time constant CNN-based spectrometry for biomedical applications. Sensors 23, 6658 (2023). https://doi.org/10.3390/s23156658

32. Szegedy, Ch., Ioffe, S., Vanhoucke, V. & Alemi, A. Inception-v4, Inception-ResNet and the impact of residual connections on learning ‌https://arxiv.org/pdf/1602.07261v2.pdf (2016).

33. ‌Takhar, D. et al. A Compressed Sensing Camera: New Theory and An Implementation Using Digital Micromirrors. in Proc. Comput. Imaging IV SPIE Electronic Imaging 1–10 (SPIE, 2006). https://doi.org/10.1117/12.659602

34. ‌Urbaś, S. & Więcek, B. Development of low-resolution, low-power and low-cost infrared System. Pomiary Autom. Robot. 25, 47–52 (2021). https://doi.org/10.14313/PAR_240/47

35. ‌Wang, Z., Bovik, A. C., Sheikh, H. R. & Simoncelli, E. P. Image quality assessment: from error visibility to structural similarity. IEEE Trans. Image Process. 13, 600–612 (2004). https://doi.org/10.1109/TIP.2003.819861

36. ‌Chollet, F. Keras (2015). https://keras.io

37. ‌Urbaś, S., Więcek, P. & Więcek, B. Simulation of Single-Pixel IR Camera With CNN Reconstruction Algorithm. in 16th Quantitative InfraRed Thermography Conference (QIRT) (QIRT Council, 2022). https://www.ndt.net/article/qirt2022/papers/2017.pdf

38. ‌Teledyne Flir (Dec. 7th, 2023) https://www.flir.eu

39. ‌Bakurov, I., Castelli, M., Buzzelli, M. & Schettini, R. Parameters Optimization of The Structural Similiarity Index. in Proc. IS&T London Imaging Meeting 2020: Future Colour Imaging 19–23 (Society for Imaging Science and Technology, 2020). https://doi.org/10.2352/issn.2694-118X.2020.LIM-13

40. ‌Olbrycht, R. A novel method for sensitivity modelling of optical gas imaging thermal cameras with warm filters. Quant. Infrared Thermogr. J. 19, 331–346 (2022). https://doi.org/10.1080/17686733.2021.1962096