Symmetry of polychromatic beams and transverse energy flows

1. Chernivtsi University, 2 Kotsybinsky Str., Chernivtsi 12, 58012, Ukraine

Abstract

The article considers the mechanisms of the formation of transverse energy flows in polychromatic fields with different structures. It is shown that the magnitude of the Poynting vector transverse component and the angular momentum for symmetric polychromatic beams are the same as in coherent monochromatic fields. Changes in the characteristics of energy flows due to the transformation and destruction of beam symmetry are demonstrated. The data of computer simulation are presented.

Introduction

This article deals with the energy flows arising in optical polychromatic waves. The study of the problem is closely connected with the relatively recent direction of modern optics, the development of optical tweezers, modern free-space communication (FSO), etc. (see, for example, Ref. 1–4).

It should be noted that the functionality of optical tweezers is determined by distribution of the characteristics of the Poynting vector transverse component, namely its modulus magnitude and azimuth distribution of this vector. In this case, the magnitude of the vector modulus both for a field of a general type, including “random” distributions of the vector parameters and for beams with an “ordered” structure is determined by the same relations for one wavelength. At the same time, as shown in Ref. 5, for polychromatic wave and paraxial approximation, the components of the time-averaged Poynting vector can be written as:

\( \bar{P}_l=\int_0^{\infty} \bar{P}_l(\lambda) d \lambda \) (1)

where 𝑙 = 𝑥, 𝑦, 𝑧, and 𝑃 ̅𝑙(𝜆) are the spectral components corresponding to the those of the Poynting vector.

The same statement is true for the angular momentum. The resulting angular momentum is defined as the sum of the corresponding spectral components:

\( M=\int_0^{\infty} M(\lambda) d \lambda \) (2)

Following from (1), the resulting magnitude of the Poynting vector modulus depends on distribution of its parameters in the spectral components, degree of their similarity, location of the “reference” points of such distributions – Poynting singularities [6, 7] in which the modulus of the vector is equal to zero, and the azimuth is undefined.

This research is an attempt to establish certain regularities in the formation of the resulting Poynting vector in ordered polychromatic fields and those of a general type.

Mechanisms of the Poynting vector formation in the fields of general type and those of ordered beams

In their analysis, the authors consider the next main issues:

1. Each spectral component forms its distribution of the characteristics of the Poynting vector
2. The resulting transverse component of the vector is formed as a simple sum of “spectral” vectors.

According to the above statements, there is an obvious difference in the formation of a vector for the general type fields and those of the ordered waves. In this sense, two boundary cases of the field structure can be identified:

• fields of general type (like speckle fields),
• elementarily symmetrical beams.

In this research, elementarily symmetrical polychro-matic beams are those for which the transverse components of the Poynting vector corresponding to different spectral components are collinear in each point of the field. These include the beams with central symmetry in the optical parameters distribution such as:

• Gaussian elliptically polarized beam (see, for example, Refs. 6, 8–10),
• white vortex (see, for example, Refs. 11 and 12),
• full Poincaré beam (see, for example, Refs. 6, 13–17).

Such beams also include polychromatic edge disloca-tions – such as polychromatic modes of the TE01(10) type and similar beams [18]. However, the topological charge of each spectral component of an edge dislocation is zero. Consequently, such a beam does not create angular momentum. Therefore, the authors exclude such beams from their consideration.

There are similar reasons for the so-called radially or azimuthally polarized beams (see, for example, Refs. 6, 14, 17–19). All beams having several Poynting singularities in their spectral components (for example, chains of vortices), even those characterised by central symmetry of parameters, belong to another class of beams that the authors call “ordered beams”.

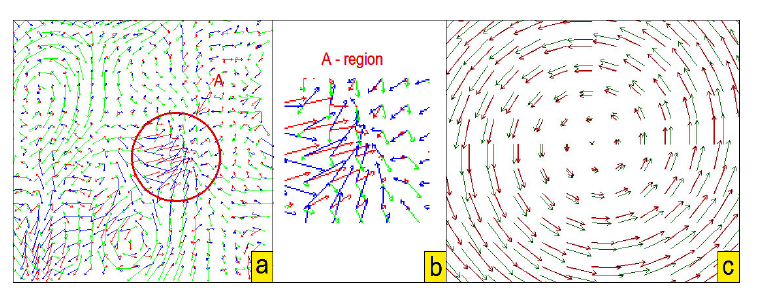
It can be stated that for a general field, the resulting Poynting vector component is the sum of quasi-randomly directed vectors with different modules at each point of the field [Fig. 1(a)]. Therefore, the average value of the resulting Poynting vector modulus is significantly lower than that in the coherent case if the powers of coherent and polychromatic beams are comparable. The situation is different when dealing with an ordered polychromatic beam.

The highest order is in the elementarily symmetrical polychromatic beams with the central symmetry of the characteristics of all spectral components [Fig. 1(b)]. For such a beam, partial spectral Poynting vectors at each point are collinear. Accordingly, the modules of the vectors are summed up like in the coherent case and the magnitude of the component is maximal.

‌

However, this situation is not always the case for beams with a central symmetry of wave parameters. Different wavelengths have their own distributions of vector characteristics, and they differ at least in scale. For example, the authors consider the Poynting vector distributions for the red and blue components of the vortex chains (see Fig. 2). As can be seen, there is at least a decrease in the resulting average magnitude of the modulus of the Poynting vector component compared to the coherent case. Such cases will be referred to as the formation of the ordered polychromatic beams. In terms of the formation of transverse energy flows, such beams occupy an intermediate place between general type fields and elementarily symmetrical polychromatic beams because a sufficiently large magnitude of the Poynting vector is preserved.

‌

Poynting vector and angular momentum of elementarily symmetrical polychromatic beams

Let us consider a well-known fact: if a significant angular momentum is formed in the vicinity of a certain point of the field, then the circulation of the Poynting vector is observed in this region (see Fig. 3 and, for example, Ref. 6). At the same time, analysing the behaviour of the vector characteristics does not allow to determine the consequence of which type of angular momentum (orbital or spin [6–8, 10]) such circulation is. Due to that, the choice of a specific beam type is not sufficient for consideration of fields with “elementary” symmetry. Therefore, the authors choose a circularly polarized polychromatic Gaussian beam and white vortex as a polychromatic beam with “elementary” symmetry of characteristics and some angular momentum.

‌

Let us consider the transverse component of the Poynting vector and the angular momentum of such beams.

It is well known that Ref. 20 is used to define the instantaneous Poynting vector:

\( \vec{P}=\vec{E} \times \vec{H} \) (3)

where 𝐸⃗ ,𝐻⃗ are respectively the strengths of electric and magnetic fields .

In the case of polychromatic waves, this relation is rather cumbersome; this does not allow for carrying out a simple and detailed analysis. Moreover, the calculation of angular momentum is not a simple task, too.

The situation is essentially simplified if the paraxial approximation is valid.

The complex amplitudes of spectral components of a Gaussian beam and an isotropic white vortex can be described as follows:

1. Gaussian beam. For simplicity, the authors will consider a Gaussian beam in the waist region or in the far zone where the radius of the phase front curvature is sufficiently large and the beam wavefront in the paraxial region is almost flat. Orthogonal components of a Gaussian beam:

   \( U_{G \lambda}(x, \mathrm{y})=f(\lambda) \frac{1}{\sigma_0} \exp \left(-\frac{x^2+y^2}{2 \sigma_0^2}\right) \exp \left(j \Phi_{0 \lambda}\right) \) (4)

2. White vortex:

   \( \begin{aligned} U_{V \lambda}(x, y)= & f(\lambda) \frac{\sqrt{x^2+y^2}}{\sigma_0} \exp \left(-\frac{x^2+y^2}{2 \sigma_0^2}\right) \\ & \times \exp \left[j\left(\operatorname{Sarctan} \frac{y}{x}\right)+\Phi_{0 \lambda}\right], \end{aligned} \) (5)

   where

   \( f(\lambda)=\frac{1}{\sigma_\lambda \sqrt{2 \pi}} \exp \left[-\frac{(\lambda-\bar{\lambda})^2}{2 \sigma_\lambda^2}\right] \) (6)

is the distribution of spectral components over the wave-lengths of the spectrum, 𝜎0 – the beam width (the same for all spectral components), 𝜆 – the wavelength, 𝜆̅ – the central (main) wavelength, Φ0𝜆 – the initial phase shift specific for each component, 𝜎𝜆 determines the width of the spectral interval, S – the topological charge of vortex.

As can be seen from (6), the contribution of spectral components is regulated by the normal law. Naturally, this is not entirely true since negative wavelengths do not exist. At the same time, it will be assumed that the spectrum drops rather quickly while moving away from the central wavelength towards small wavelengths and the influence of “negative” wavelengths is negligible.

The authors will analyse a circularly polarized beam as an elementarily symmetrical polychromatic Gaussian beam. This assumption does not reduce the generality of the consideration, since the ellipticity of the beam affects only the finite value of the transverse component of the Poynting vector. The component of the beam with circular polarization is maximum. In this case, the phase difference between the beam 𝑥- and 𝑦- components is written as [20]:

\( \Delta \Phi=\Phi_y-\Phi_x=h \pi / 2 \) (7)

where ℎ is the handedness factor equal to + 1 for the right polarization and −1 for the left one.

Poynting vector of an elementarily symmetric polychromatic beam

It should be mentioned that the resulting Poynting vector of a polychromatic wave, according to (4), is the sum of the corresponding spectral components. Therefore, for the first stage analysis, it is enough to define the transverse components of the spectral components as coherent, and then sum them up.

The transverse spectral components of the time-averaged Poynting vector are defined by relations [6]:

\( \left\{\begin{array}{l} \bar{P}_{x \lambda}=\frac{c \lambda}{32 \pi^2}\left\{\left[\left(s_0+s_1\right) \frac{\partial \Phi_{x \lambda}}{\partial x}+\left(s_0-s_1\right) \frac{\partial \Phi_{y \lambda}}{\partial x}\right]-\frac{\partial s_{3 \lambda}}{\partial y}\right\} \\ \bar{P}_{y \lambda}=\frac{c \lambda}{32 \pi^2}\left\{\left[\left(s_0+s_1\right) \frac{\partial \Phi_{x \lambda}}{\partial y}+\left(s_0-s_1\right) \frac{\partial \Phi_{y \lambda}}{\partial y}\right]+\frac{\partial s_{3 \lambda}}{\partial x}\right\} \end{array}\right. \) (8)

where 𝑠𝑖, 𝑖=0, 1, 2, 3 – the normalised Stokes para-meters, Φ𝑙𝜆 – the components phases (𝑙=𝑥,𝑦).

Transverse components of the Poynting vector of a scalar wave are

\( \left\{\begin{array}{l} \bar{P}_{x \lambda}=\frac{c \lambda A_\lambda^2}{16 \pi^2} \frac{\partial \Phi_\lambda}{\partial x} \\ \bar{P}_{y \lambda}=\frac{c \lambda A_\lambda^2}{16 \pi^2} \frac{\partial \Phi_\lambda}{\partial y} \end{array}\right. \) (9)

where 𝐴𝜆,Φ𝜆 – the corresponding amplitude modulus and phase.

Transverse components of the Poynting vector of a polychromatic Gaussian beam

Considering the fact that Gaussian beams are taken under consideration, the phase front of which is almost flat, the derivatives in (8) are equal to zero. Then,

\( \left\{\begin{array}{l} P_{x \lambda}=-\frac{c \lambda}{32 \pi^2} \frac{\partial s_{3 \lambda}}{\partial y} \\ P_{y \lambda}=\frac{c \lambda}{32 \pi^2} \frac{\partial s_{3 \lambda}}{\partial x} \end{array}\right. \) (10)

or

\( \left\{\begin{array}{l} P_{x \lambda}=-\frac{c \lambda}{32 \pi^2} \frac{\partial A_{x \lambda} A_{y \lambda} \sin \Delta \Phi}{\partial y} \\ \bar{P}_{y \lambda}=\frac{c \lambda}{32 \pi^2} \frac{\partial A_{x \lambda} A_{y \lambda} \sin \Delta \Phi}{\partial x} \end{array}\right. \) (11)

In the authors’ case:

1. ΔΦ=ℎ𝜋/2 and sinΔΦ=ℎ.

2. \( A_{\xi x \lambda}=A_{G y \lambda}=\frac{1}{\sigma_0 \sigma_\lambda \sqrt{2 \pi}} \exp \left[-\frac{(\lambda-\bar{\lambda})^2}{2 \sigma_\lambda^2}\right] \exp \left(-\frac{x^2+y^2}{2 \sigma_0^2}\right) \) (12)

Then, equation (11) is transformed to the form:

\( \left\{\begin{array}{l} \bar{P}_{x \lambda}=h y \frac{c \lambda}{32 \pi^3 \sigma_0^4 \sigma_\lambda^2} \exp \left[-\frac{(\lambda-\bar{\lambda})^2}{\sigma_\lambda^2}\right] \exp \left(-\frac{x^2+y^2}{\sigma_0^2}\right) \\ \bar{P}_{y \lambda}=-h x \frac{c \lambda}{32 \pi^3 \sigma_0^4 \sigma_\lambda^2} \exp \left[-\frac{(\lambda-\bar{\lambda})^2}{\sigma_\lambda^2}\right] \exp \left(-\frac{x^2+y^2}{\sigma_0^2}\right) \end{array}\right. \) (12)

Naturally, for a coherent Gaussian circularly polarized beam, the transverse components of the Poynting vector are defined by the relations:

\( \left\{\begin{array}{l} \bar{P}_{x \lambda}=h\left[\frac{c \lambda}{32 \pi^2 \sigma_0^2} \exp \left(-\frac{x^2+y^2}{\sigma_0^2}\right)\right] y \\ \bar{P}_{y \lambda}=-h\left[\frac{c \lambda}{32 \pi^2 \sigma_0^2} \exp \left(-\frac{x^2+y^2}{\sigma_0^2}\right)\right] x \end{array}\right. \) (13)

For the authors’ case, following (4), the resulting components of the Poynting vector will be written as:

\( \left\{\begin{array}{l} P_x=h y \frac{c}{32 \pi^3 \sigma_0^2 \sigma_\lambda^2} \exp \left(-\frac{x^2+y^2}{\sigma_0^2}\right) \int_{-\infty}^{\infty} \lambda \exp \left[-\frac{(\lambda-\bar{\lambda})^2}{\sigma_\lambda^2}\right] d \lambda \\ P_y=-h x \frac{c}{32 \pi^3 \sigma_0^2 \sigma_\lambda^2} \exp \left(-\frac{x^2+y^2}{\sigma_0^2}\right) \int_{-\infty}^{\infty} \lambda \exp \left[-\frac{(\lambda-\bar{\lambda})^2}{\sigma_\lambda^2}\right] d \lambda \end{array}\right. \) (14)

It can be shown [21] that the integral is:

\( I=\int_{-\infty}^{\infty} \lambda \exp \left[-\frac{(\lambda-\bar{\lambda})^2}{\sigma_\lambda^2}\right] d \lambda=\sigma_\lambda \sqrt{\pi} \bar{\lambda} \) (15)

Then, the final expression for the transverse compo-nents of the Poynting vector has the form:

\( \left\{\begin{array}{l} P_x=\frac{\sqrt{\pi}}{\sigma_\lambda} h\left[\frac{c \bar{\lambda}}{32 \pi^2 \sigma_0^2} \exp \left(-\frac{x^2+y^2}{\sigma_0^2}\right)\right] y \\ \bar{P}_y=-\frac{\sqrt{\pi}}{\sigma_\lambda} h\left[\frac{c \bar{\lambda}}{32 \pi^2 \sigma_0^2} \exp \left(-\frac{x^2+y^2}{\sigma_0^2}\right)\right] x \end{array}\right. \) (16)

which, up to a constant coefficient √𝜋/𝜎𝜆, indicating that the beam is formed as a polychromatic one, corresponds to the expression for a coherent circularly polarized beam (13). Accordingly, the angular momentum of the Gaussian polychromatic beam is the same as in the coherent case.

Transverse components of the Poynting vector of a polychromatic vortex beam

Considering (4), (5), (11) and relations for derivatives:

\( \frac{\partial \Phi_\lambda}{\partial x}=-S \frac{1}{x^2+y^2} y, \ldots \quad \frac{\partial \Phi_\lambda}{\partial y}=S \frac{1}{x^2+y^2} x \) (17)

it can be easily shown that the spectral components of the Poynting vector are described by the relation:

\( \left\{\begin{array}{l} \bar{P}_{x \lambda}=-S y \frac{c \lambda}{32 \pi^3 \sigma_0^2 \sigma_\lambda^2} \exp \left[-\frac{(\lambda-\bar{\lambda})^2}{\sigma_\lambda^2}\right] \exp \left(-\frac{x^2+y^2}{\sigma_0^2}\right) \\ \bar{P}_{y \lambda}=S x \frac{c \lambda}{32 \pi^3 \sigma_0^2 \sigma_\lambda^2} \exp \left[-\frac{(\lambda-\bar{\lambda})^2}{\sigma_\lambda^2}\right] \exp \left(-\frac{x^2+y^2}{\sigma_0^2}\right) \end{array}\right. \) (18)

which, to the signs and value of the topological charge 𝑆, coincides with (12). As a result, the resulting Poynting vector is described similarly to (16).

In other words, a polychromatic Gaussian beam and a white vortex of the same width create angular momenta of the same magnitude if the signs of the handedness factor and the topological charge are different, i.e.:

\( h=-S \) (19)

Full Poincaré beam

As in the coherent case, a Full Poincaré beam (a polarization-inhomogeneous wave structure with an isolated C-point) can be synthesized as a superposition of an orthogonally circularly polarized Gaussian beam and an isotropic vortex [6, 16]. In other words, based on the considerations presented in sections 5 and 6, it can be argued that in this situation, the behaviour of the transverse components of the Poynting vector is the same as in the coherent case.

Influence of beam symmetry destruction on the magnitude of the transverse component of the Poynting vector of a polychromatic wave

It has been noted that symmetry of elementarily symmetrical polychromatic beams may be destructed due to beam propagation through the medium with some physical perturbations.

Focusing on the analysis given in section 3, it is possible to formulate the following hypothesis. If the authors have a polychromatic beam that satisfies their definition of elementary symmetric beams, then, with the destruction of such symmetry, the average magnitude of the modulus of the Poynting vector transverse should decrease. Such a hypothesis does not need to be proved. At the same time, when the symmetry is broken, one can single out the so-called “intermediate” stages, e.g., the transformation of a higher-order symmetry into a lower-level symmetry

The question arises: will there be a decrease in the modulus of the Poynting vector component as it was in the case of chaotization of the spectral characteristics distributions of the wave components?

Rather conventionally, two main types of symmetry can be distinguished (see Ref. 22):

1. central symmetry
2. axial symmetry

Central symmetry is considered a higher class of symmetry than the axial one. As shown in section 3, the behaviour of the Poynting vector in fields with “elementary” central symmetry of the spectral components hardly differs from the behaviour of this vector in coherent analogues.

Therefore, to assess the influence of such symmetry destruction on the polychromatic beam characteristics, two processes will be considered:

1. transformation of beams with central symmetry of parameters into those with axial symmetry,
2. “chaotic” transformation of spectral components – complete loss of the symmetrical properties of a poly-chromatic beam.

It should be noted that in the coherent case, physical perturbations along the optical path, as a rule, do not destroy the structure of optical parameters distributions, but rather lead to their spatial deformation while maintaining the main features of such distributions. An exception to this is the destruction of topological defects like vortices with a charge greater than unity, etc. There is also no decrease in the value of the transverse component of the Poynting vector. Therefore, the main factor that determines changes in the structure of the energy flows of a polychromatic wave is the mutual displacement of singular points (vortices of Poynting singularities, etc.) in different spectral components. Then, the corresponding changes in the distri-bution of the characteristics of the transverse component of the Poynting vector under such chaotization or symmetry transformation of polychromatic wave characteristics are considered.

It is necessary to state that it is rather difficult to analyse such changes in symmetric beams in general terms. At the same time, the behaviour of the Poynting vector in such beams is similar. For example, as it was mentioned before, the circulation of the transverse component observed in circularly polarized beams and near the centre of vortex beams are identical. Accordingly, to estimate the influence of such factors as the symmetry of the beam parameters on the distribution of the transverse component of the Poynting vector, it would be enough to demonstrate it for one type of beam, e.g., for a beam of the white vortex type.

Fig. 4 illustrates schemes for chaotic and regular destruction of beam symmetry. The yellow square identifies the initial position of the centres of all spectral vortices. Squares of other colours show the displacement of symmetry. The transformation of a white vortex of a beam with central symmetry into that with axial symmetry of spectral vortices centres due to the destruction of the beam components may occur due to the propagation of this beam through some optical system, e.g., through the system presented in Fig. 5(a). A similar shift between components will be observed if the beam passes through a sufficiently thick plane-parallel plate located at a certain angle to the beam axis. Another example is a diffraction of a white vortex at the edge of the screen [Fig. 5(b)]. It is known, that in such situation, the monochromatic vortex centre shifts [23–27]. The magnitude of the shift depends on the wavelength.

‌ ‌

The chaotic destruction of symmetry can be performed by passing the beam through a medium with random physical perturbations depending on the wavelength.

The “degree” of transformation (destruction) of the symmetry is set by the magnitude of the average shift of the spectral components Δ𝑠̅̅̅. To compare the influence of both types of beam transformation, it is sufficient that the following condition is satisfied: where Δ𝑠̅̅̅ reg,Δ𝑠̅̅̅ rand – the averaged shift of spectral components for regular and randomly shifted components.

The authors made the corresponding computer simula-tion for a polychromatic beam of the white vortex type. The simulation results are shown in Fig. 6. Figures 6(a) and (b) illustrate the distribution of the characteristics of the transverse component of the Poynting vector in a white vortex, in a situation where there is no shift in the spectral components. As it was shown in section 3, the modulus (its magnitude) and the azimuth of this vector are distributed in the same way as in the coherent case. Fig. 6, columns (c–o) and (d–p) correspond to the regular transformation of the beam, the transition from central to axial symmetry. Fig. 6(c–o) correspond to intensity distributions in the transformed beam. Fig. 6(d–p) show how the magnitudes and azimuths of the resulting Poynting vector change. The value of the regular shift increases in the direction from the top to the bottom of Fig. 6.

‌

Fig. 6, columns (e–m) and (f–n) illustrate changes in the intensity distributions (e–m) and the Poynting vector characteristics (f–n) under the random shift of the spectral components. As in the previous case, the average value of the random shift of the components increases from the top to the bottom of Fig. 6.

The value of the average shift is given in parts of the width of the initial beam σ. For a vortex beam, including the white vortex and its spectral components, the beam intensity at a distance σ from the centre of the vortex is maximum.

The simulation results given in one line of Fig. 6 corres-pond to the fulfilment of (20). As can be seen from Fig. 6:

1. The beam intensity distribution undergoes significant changes. The zero minimum at the centre of the beam vanishes even for slight shifts of the centres of the spectral components (both for regular and random shifts).
2. At the same time, the magnitude of the transverse component of the Poynting vector remains equal to zero, even with a significant shift of the spectral components. Thus, even at shifts of the order of 0.4σ (for any shift nature), circulation of the transverse component of the Poynting vector is observed. However, it is worth noting that in the case of a random shift, changes in the behaviour of the beam charac-teristics occur much faster than in the transition from central to axial symmetry. For example, for a random shift of the order of 0.25σ, instead of a minimum, a maximum is formed at the centre of the beam. At the same time, with a regular shift of the components, a maximum is retained at the centre of the beam, which is observed even for significant shifts (see Fig. 6).

The general conclusion can also be substantiated by the fact that at the broken symmetry, the magnitude of the modulus of the transverse component of the Poynting vector decreases faster than at the transformation of the beam symmetry type. Fig. 7 illustrates this fact. It can be seen from Fig. 7 that even with a regular shift of the centres of the spectral components of the 0.8σ order, the compo-nent modulus remains about 60% of the initial magnitude.

‌

If one considers that for a general type field and for complete destruction of the temporal coherence of a poly-chromatic wave [5], the magnitude of the transverse component tends to small value [about 20% of coherent magnitude, see Fig. 8(a)], and with additional destruction of spatial coherence it is close to zero, then, one can draw a general conclusion. Only for elementarily symmetrical polychromatic beams, the magnitude of the transverse component of the Poynting vector is similar to that of coherent waves. For all other wave types, this value decreases as it is qualitatively shown in Fig. 8(b).

‌

Conclusions

1. Only for elementarily polychromatic fields, the trans-verse component of the Poynting vector and the angular momentum have the same magnitudes as in the coherent case.
2. When the symmetry is transformed from a higher-order symmetry to a lower one (central to axial), or the central symmetry of the beam characteristics is destroyed, the magnitude of the transverse component of this vector decreases up to zero in polychromatic fields of general type.
3. When the symmetry is transformed, the magnitude of the transverse component of the Poynting vector remains significant. For small shifts of the spectral components (about half of the beam width), it is at least 50% of the initial magnitude.
4. When the symmetry of a polychromatic beam is destroyed chaotically, the decrease of the transverse component magnitude occurs much faster (at least by a factor of 2–2.5) until it completely disappears in the fields of general type.

References

1. ‌McGloin, D. Optical tweezers: 20 years on. Philos. Trans. R. Soc. A364, 3521–3537 (2006). https://doi.org/10.1098/rsta.2006.1891

2. Lang, M. J. & Block, S. M. Resource letter: LBOT-1: Laser-based optical tweezers. Am. J. Phys. 71, 201–215 (2003). https://doi.org/10.1119/1.1532323

3. D’Amico, M., Leva, A. & Micheli, B. Free-space optics communication systems: First results from a pilot field-trial in the surrounding area of Milan, Italy. IEEE Microw. Wirel. Compon. Lett. 13, 305–307 (2003). http://dx.doi.org/10.1109/LMWC.2003.815699

4. ‌Gibson, G. et al. Free-space information transfer using light beams carrying orbital angular momentum. Opt. Express 12, 5448–5456 (2004). https://doi.org/10.1364/OPEX.12.005448

5. ‌Mokhun, I. et al. Energy flows in polychromatic fields. J. Opt. 23, 015401 (2020). https://doi.org/10.1088/2040-8986/abcc54

6. ‌Mokhun, I. I. Introduction to Linear Singular Optics. Chapter 1. in Optical correlation techniques and applications (ed. Angelsky O. V.) 1–131 (SPIE Press, Bellingham, Washington, 2007).

7. ‌Mokhun, I., Mokhun, A. & Viktorovskaya, J. Singularities of Poynting vector and the structure of optical fields. Ukr. J. Phys. Opt. 7, 129–141 (2006). https://doi.org/10.3116/16091833/7/3/129/2006

8. ‌Allen, L., Padgett, M. J. & Babiker, M. IV The orbital angular momentum of light. Prog. Opt. 39, 291–372 (1999). https://doi.org/10.1016/S0079-6638(08)70391-3

9. ‌Mokhun, I., Arkhelyuk, A. D., Galushko, Y., Kharitonova, Y. & Viktorovskaya, Y. Angular momentum of incoherent Gaussian beam. Appl. Opt. 53, B38–B42 (2014). https://doi.org/10.1364/AO.53.000B38

10. ‌Bekshaev, A., Bliokh, K. & Soskin, M. Internal flows and energy circulation in light beams. J. Opt. 13, 053001 (2011). https://doi.org/10.1088/2040-8978/13/5/053001

11. ‌Berry, M. V. Coloured phase singularities. New J. Phys. 4, 1–66 (2002).https://doi.org/10.1088/1367-2630/4/1/366

12. ‌Angelsky, O. V., Maksimyak, A. P., Maksimyak, P. P. & Hanson S. G. Interference diagnostics of white-light vortices. Opt. Express13, 8179–8183 (2005). https://doi.org/10.1364/OPEX.13.008179

13. ‌Beckley, A. M., Brown, T. G. & Alonso, M.A . Full Poincaré beams. Opt. Express 18, 10777–10785 (2010).https://doi.org/10.1364/OE.18.010777

14. ‌Senthilkumaran, P. Singularities in Physics and Engineering. Properties, Methods, and Applications. (IOP Publishing Ltd, 2018).

15. ‌Mokhun, I. & Khrobatin, R. Shift of application point of angular momentum in the area of elementary polarization singularity. J. Opt. A Pure Appl. Opt. 10, 064015 (2008).https://doi.org/10.1088/1464-4258/10/6/064015

16. ‌Dennis, M. R., O’Holleran, K. & Padgett, M. J. Singular optics: optical vortices and polarization singularities. Prog. Opt. 53, 293– 363 (2009). https://doi.org/10.1016/S0079-6638(08)00205-9

17. ‌Mokhun, I. et al. Formation of Polychromatic Edge Dislocation. in 15th International Conference on Correlation Optics vol. 12126 (SPIE, 2021).

18. ‌Nesterov, A. V. & Niziev, V. G. Laser beams with axially symmetric polarization. J. Phys. D: Appl. Phys. 33, 1817–1822 (2000). https://doi.org/10.1088/0022-3727/33/15/310

19. ‌Lerman, G. M., Lilach, Y. & Levy, U. Demonstration of spatially inhomogeneous vector beams with elliptical symmetry. Opt. Lett. 34, 1669–1671 (2009). https://doi.org/10.1364/OL.34.001669

20. ‌Born, M. & Wolf, E. Principles of Optics. Sixth edition. (Oxford: Pergamon, 1980).

21. ‌Prudnikov, A. B, Brychkov, Y. A. & Marichev, O. I. Integrals and Series. First edition. (CRC Press, 1992).

22. ‌The Language of Symmetry. (eds. Rattigan, B., Noble, D. & Hatta, A.) 138 (Chapman & Hall, 2023).

23. ‌Bekshaev, A. Y. & Sviridova, S. V. Effects of misalignments in the optical vortex transformation performed by holograms with embedded phase singularity. Opt. Commun. 283, 4866–4876 (2010). https://doi.org/10.1016/j.optcom.2010.07.031

24. ‌Zwillinger, D. & Jeffrey, A. Table of Integrals, Series, and Products. 7th Edition. (Academic Press, 2007).

25. ‌Vasnetsov, M. V., Marienko, I. G. & Soskin, M. S. Self- reconstruction of an optical vortex. J. Exp. Theor. Phys. Lett. 71, 130–133 (2000). https://doi.org/10.1134/1.568297

26. ‌Masajada, J. Half-plane diffraction in the case of Gaussian beams containing an optical vortex. Opt. Commun. 175, 289–294 (2000). https://doi.org/10.1016/S0030-4018(00)00470-3

27. ‌Bekshaev, A. Y., Mohammed, K. A. & Kurka, I. A. Transverse energy circulation and the edge diffraction of an optical-vortex beam. Appl. Opt. 53, B27–B37 (2014).